Perioada sărbătorilor de iarnă este plină de veselie, iar stresul de a cumpăra și a împacheta cadouri de Crăciun, de a organiza petrecerea perfectă și de a împodobi bradul nu ar trebui să te descurajeze.
1. Cum să îți faci cumpărăturile pentru Crăciun?

Dacă aveți o listă lungă cu familia și prietenii, dar fondurile bancare sunt limitate, pentru cine ar trebui să cumpărați cadouri?
Prof. Rachel Norman și dr. Anthony O’Hare, din cadrul Universității din Stirling, au aplicat teoria jocurilor la schimbul de cadouri. Teoria jocurilor reprezintă o ramură a matematicii, care are legătură cu calcularea strategiilor optime în situații competitive. Elementul central este ideea de a găsi „echilibrul Nash” inexploatabil. Dacă doi oameni joacă amândoi strategia Nash, atunci niciunul dintre ei nu-și poate îmbunătăți probabilitatea de reușită schimbând abordarea.
Să presupunem că primirea unui cadou invocă plăcerea, E, iar acordarea cadoului are costul C. Diagrama de mai sus prezintă posibilele beneficii pentru două persoane. De exemplu, dacă jucătorul 1 oferă cadou, dar jucătorul 2 nu, atunci jucătorul 1 primește valoarea C_1 (un cost net) în timp ce jucătorul 2 nu are niciun cost, dar se bucură având E_2.
Echilibrul Nash din situația respectivă este reprezentat de faptul că ambii jucători nu ar trebui să își ofere cadouri. Astfel, plata pentru fiecare este zero, iar dacă oricare dintre aceștia deviază unilateral, nu va mai fi un echilibru.
Această teorie presupune ca activitatea să fie „jucată” o singură dată. Politologul american, Robert Axelrod, a arătat că atunci când jocurile sunt jucate de multe ori, strategiile nerăbdătoare ca aceasta nu mai sunt optime. În schimb, cea mai bună plată vine dintr-o abordare denumită „represalii echivalente” – cumpărarea unui cadou la primul Crăciun și apoi, în anii următori, copierea a ceea ce a făcut cealaltă persoană ultima dată.
2. Cum se taie un tort de Crăciun?
Dacă te-ai săturat să tai tortul de Crăciun, care, între timp s-a uscat, vestea bună este că știința a găsit o modalitate simplă de a menține tortul mai proaspăt, pentru mai mult timp.
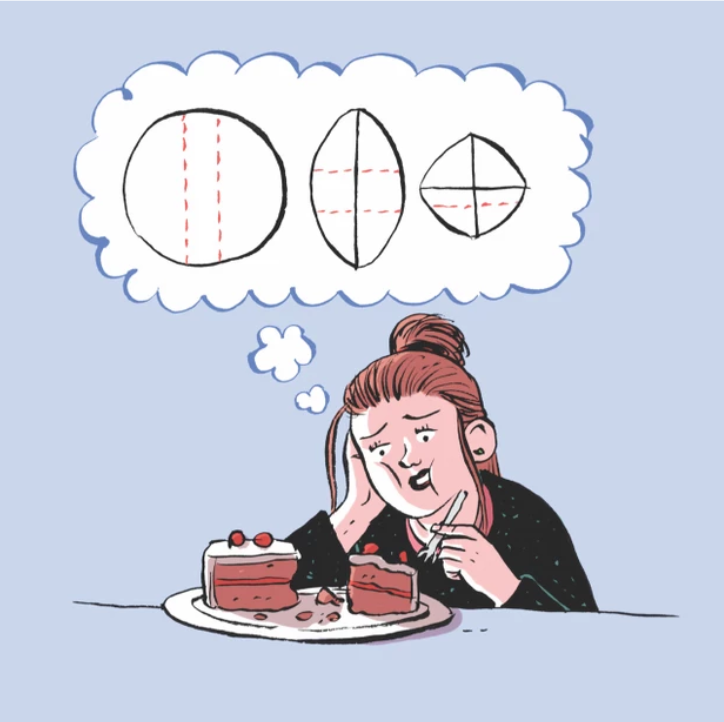
Într-o scrisoare către revista de cercetare Nature, publicată la data de 20 decembrie 1906, polimatul britanic Sir Francis Galton susținea faptul că modul tradițional de a tăia un tort de Crăciun era „foarte defectuos”. Acesta considera că scoaterea unei felii, la un moment dat, lasă suprafața interioară a tortului expusă și probabil să se usuce. În schimb, Galton a prezentat o metodă nouă de feliere a tortului, care implică efectuarea de tăieturi paralele prin centrul tortului și apoi închiderea acestuia și fixarea cu o bandă elastică, pentru a păstra prospețimea.
Acest lucru este prezentat în diagramă, adaptată dintr-o schiță care a însoțit scrisoarea originală a lui Galton. Liniile solide prezintă tăieturile existente; liniile punctate arată următoarea tăiere de realizat. Prima tăietură, situată în stânga, îndepărtează o felie plată și tortul este apoi închis în formă ovală și depozitat. Următoarea felie este îndepărtată în mod similar, dar la 90 de grade față de prima tăiere, așa cum se arată în imaginea centrală. Următoarea felie ar fi luată paralel cu prima tăietură și așa mai departe.
3. Cum se gătește un curcan?

Coacerea la cuptor a unui curcan este dificilă, deoarece carnea este alcătuită din diferite componente care, în mod ideal, necesită a fi gătite la temperaturi variate. De exemplu, carnea de piept nu trebuie încălzită la o temperatură mai mare de 55 °C, pentru a preveni întărirea acesteia, în timp ce carnea de pe pulpe trebuie să atingă cel puțin 80 °C și pielea necesită până la 200 °C pentru a declanșa Reacțiile Maillard, care rumenesc exteriorul și creează aroma caracteristică.
Prof. Peter Barham, fizician în cadrul Universității din Bristol, dar pasionat de tendințele gastronomice, susține faptul că strategia ideală este să tăiați curcanul și să gătiți fiecare parte a acestuia separat, la temperaturile optime. În cazul în care carnea de curcan tăiată nu are aspectul dorit, el sugerează să acoperiți părțile mai sensibile în folie, pentru cea mai mare parte a timpului de coacere.
Dar cât timp ar trebui să fie gătită carnea de curcan? Fizicianul regretat al Universității Stanford, Wolfgang Panofsky, a folosit legile conducției termice pentru a realiza formula t = 1,13 x W (2/3) unde t este timpul de gătit în ore și W este greutatea curcanului în kilograme. El a presupus o temperatură a cuptorului de 165 °C și un curcan cu o formă sferică.
Pentru siguranță, este recomandat să folosiți un termometru pentru carne și să vă asigurați că interiorul păsării este gătit la cel puțin 75 °C.
4. Cum să împachetezi cadourile de Crăciun?

Dr. Sara Santos, din cadrul Goldsmiths, Universitatea din Londra, a conceput o formulă pentru a calcula dimensiunile optime ale hârtiei de ambalat cadouri, pentru a acoperi o cutie cuboidă.
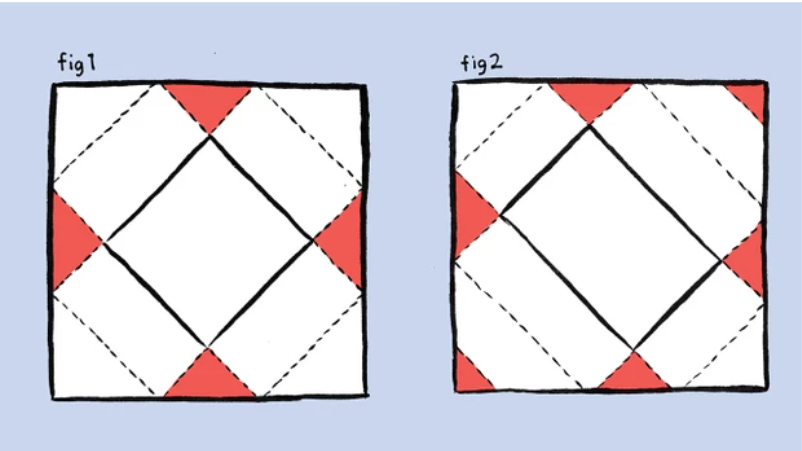
Pentru o cutie cu baza în formă de pătrat, aveți nevoie de o hârtie cu lățimea egală cu diagonala bazei cutiei, și o lungime de 1,5 mai mare decât înălțimea cutiei. Așezați cutia pe hârtie la un unghi de 45°, aduceți colțurile hârtiei în partea superioară pentru a se intersecta și fixați-o cu o singură bucată de bandă (fig 1).
Pentru o bază dreptunghiulară, utilizați o hârtie în formă pătratică, cu lungimea laterală egală cu lățimea cutiei plus lungimea acesteia plus dublul înălțimii sale, totul înmulțit cu 0,75 (fig 2).
Acestea fiind spuse, doctorii Hannah Fry și Thomas P Oléron Evans susțin, în cartea lor „Existența incontestabilă a lui Moș Crăciun”, faptul că această tehnică nu folosește mai puțină hârtie decât metoda tradițională, deși arată frumos și economisește bandă de lipit. Aceștia sugerează că o abordare mai practică este aceea de a folosi cutii mai plate pentru a reduce la minimum hârtia irosită la capetele cadoului. O cutie cu o înălțime mai mică cu 50% decât lungimea laturii de bază necesită cu 11% mai puțină hârtie decât un cub cu același volum.
5. Cum organizați un Secret Santa?
În cadrul birourilor de la muncă, oamenii organizează un eveniment de oferire a cadourilor de Crăciun, denumit Secret Santa. Aceștia își scriu numele pe bucăți de hârtie, le pun într-o pălărie și apoi extrag câte o persoană aleatorie pentru care să cumpere un cadou. Dacă cineva primește propriul nume, îl înlocuiește și extrage din nou.
Dar întregul proces trebuie reluat dacă ultima persoană care extrage își alege propriul nume. De exemplu, într-un birou de 10 persoane, acest lucru se întâmplă de peste 7,5% din timp. De asemenea, nu este perfect întâmplător.
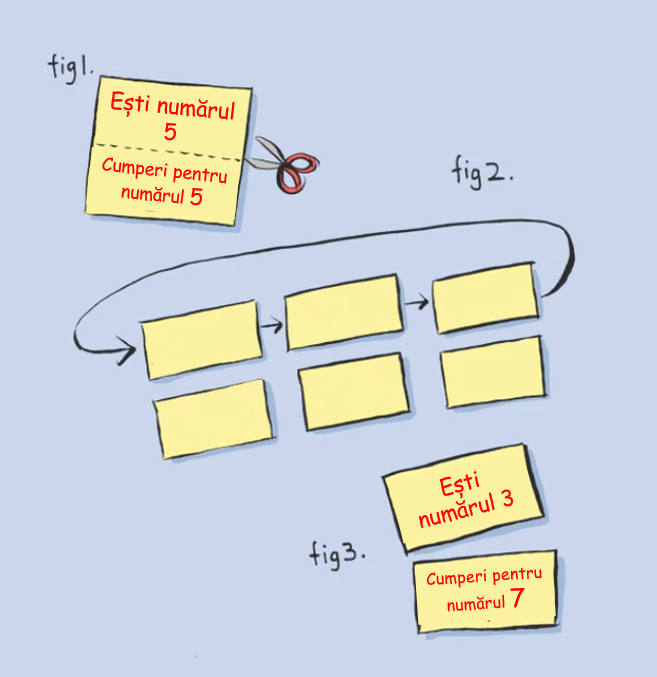
„Dacă ești ultima persoană care extrage biletul cu nume, într-un grup de trei oameni, atunci este de două ori mai probabil ca primul să-ți cumpere un cadou decât cel de-al doilea,” a declarat dr. Hannah Fry. Dar aceasta are o soluție. Creați un set de bilete, câte unul pentru fiecare persoană. Biletele ar trebui să fie asemănătore cu cele din fig 1. Așezați biletele cu fața în jos pe un singur rând, amestecați-le și, ținându-le cu fața în jos, tăiați-le în două. Acum deplasați cărțile de deasupra, o poziție spre dreapta (fig. 2).
Fiecare persoană ia un bilet din rândul de sus și altul chiar de sub acesta, spunându-le numărul personal și numărul persoanei pentru care cumpără (fig. 3). În cele din urmă, afișați o listă de numere pe perete și fiecare își scrie numele lângă numărul său. O astfel de extragere este cu adevărat anonimă și perfect aleatorie.
6. Cum decorezi un brad de Crăciun?
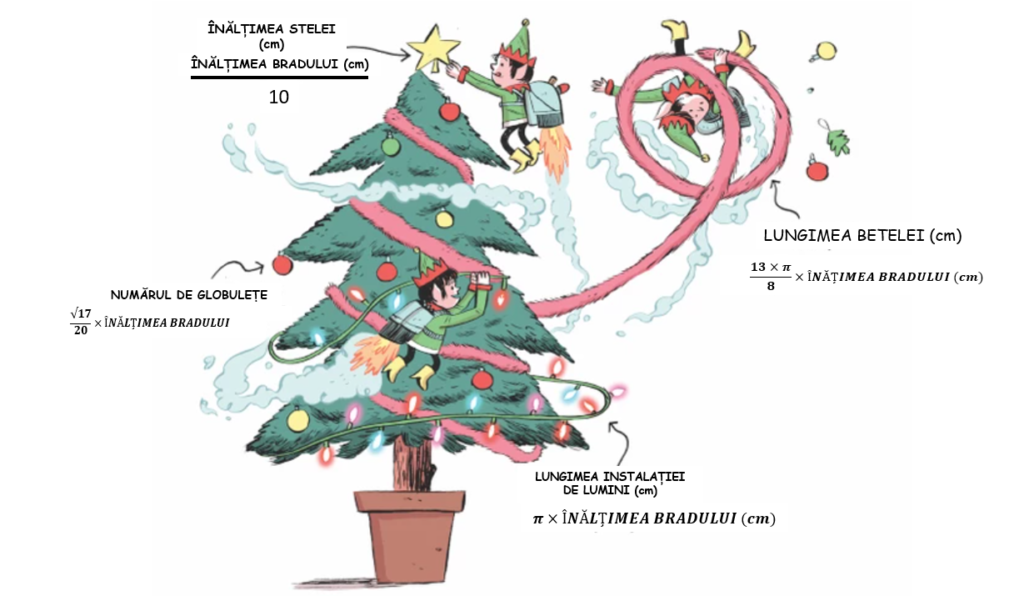
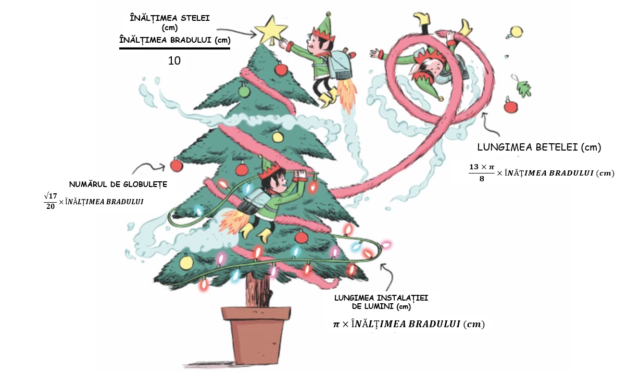
Studenții din cadrul Societății de Matematică din Universitatea Sheffield (SUMS) au dezvoltat un set de ecuații pentru a calcula cantitatea optimă de beteală, numărul de globulețe, lungimea instalației de lumini și dimensiunea stelei pentru brad, toate acestea ca funcții matematice comune, în funcție de înălțimea bradului (metoda poate fi încercată în următorul link) De exemplu, dacă bradul are o înălțime de 152 cm, atunci teoria, pe care o numesc „treegonometrie”, dictează că ar trebui să-l împodobiți cu 776 cm de beteală, 31 de baloane, o instalație de lumini cu o lungime de 478 cm, și o stea cu o înățime de 15 cm.
Însă, cum mențineți rezistența bradului? O strategie promițătoare a fost descoperită de oamenii de știință din cadrul Centrului de Cercetare a Pomului de Crăciun, Universitatea Dalhousie, Nova Scoția. În 2016, aceștia au descoperit faptul că LED-urile (în special becurile roșii și albe) emit spectrul potrivit de lumină pentru a stimula fotosinteza, permițând copacului să producă carbohidrați, oferindu-i o sursă de energie care menține ramurile atașate de copac mai mult timp.
7. Cum organizezi o petrecere de Crăciun?
Deci, aveti prieteni invitați de Crăciun, dar câți ar trebui să fie? Pentru conversații diverse, ar fi necesar trei sau mai mulți invitați care sunt străini reciproci, fie trei sau mai mulți care sunt deja cunoscuți. Deci, care este numărul minim de oameni de care aveți nevoie la petrecere, pentru a vă asigura confortul?
În anul 1928, matematicianul britanic Frank Plumpton Ramsey a găsit răspunsul cu teoria sa, privind conexiunea punctelor pe un grafic. „Numerele Ramsey” R (m, n) oferă numărul de persoane care pot fi invitate astfel încât cel puțin fie m dintre ei să se cunoască, fie n dintre ei nu. Se pare că R (3, 3) = 6.
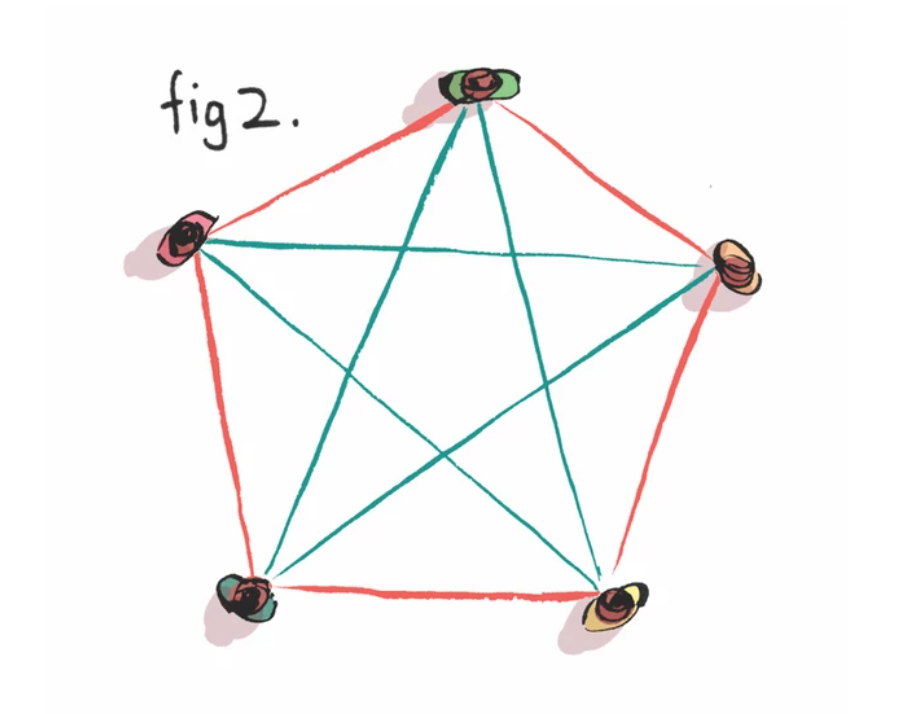
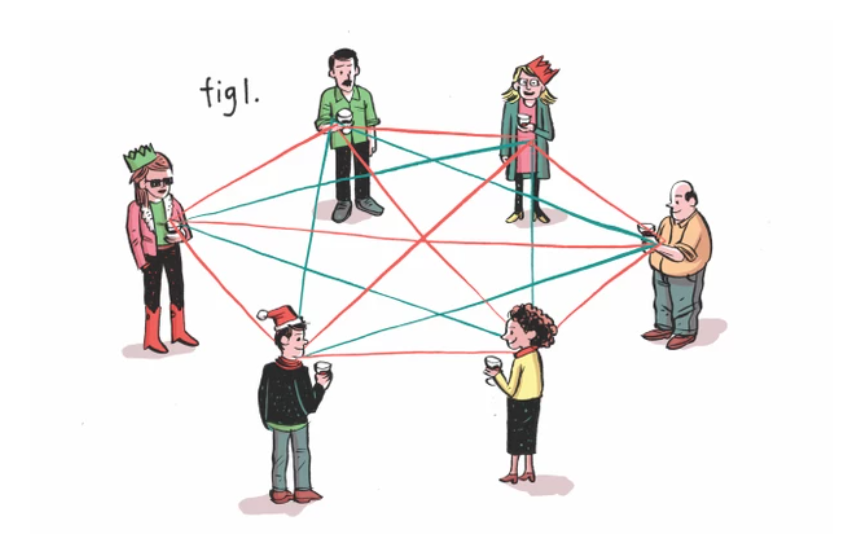
Pentru a vedea cum funcționează această teorie, desenați șase puncte pe o foaie de hârtie, fiecare reprezentând un oaspete. Trageți linii între oaspeți, roșu dacă se cunosc, albastru dacă nu se cunosc. Cu șase invitați (fig. 1) veți găsi imposibil să conectați toți oaspeții, fără a crea fie un triunghi roșu (adică trei persoane care se cunosc), fie un triunghi albastru (trei persoane străine). Dar acest lucru nu se aplică și în cazul cu doar cinci puncte (fig 2). Deci șase este numărul minim de persoane care pot fi invitate.