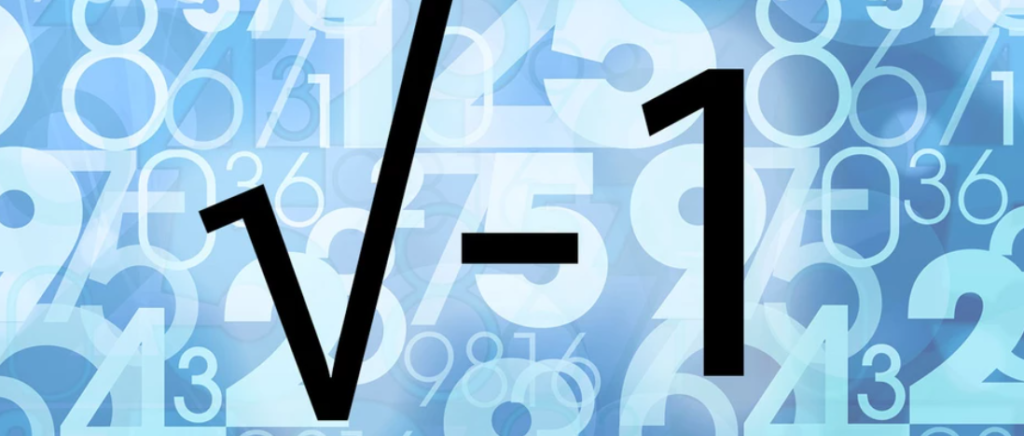În anul 1707, Abraham de Moivre, a fost printre primii care a analizat numerele complexe și geometria, elaborând o teoremă care face legătura între numerele complexe și trigonometrie.
Argand a fost, de asemenea, un pionier în studiul numerelor imaginare în raport cu geometria, utilizând conceptul de numere complexe. Acesta a dezvoltat „diagramele Argand”, care sunt asemănătoare unui grafic normal, cu axele x și y, cu mențiunea că aceste axe reprezintă numerele reale și cele imaginare. Aceste descoperiri au permis rezolvarea problemelor complexe algebrice, cu ajutorul geometriei.
Numerele complexe sunt numere alcătuite dintr-o parte reală și una imaginară. De exemplu, 4 + 2i este un număr complex, format dintr-o parte reală egală cu 4 și o parte imaginară egală cu 2i. Totodată, 17 este un număr complex, parte reală fiind egală cu 17, iar partea imaginară fiind egală cu zero, deoarece aceasta nu există.
Matematicienii folosesc litera „i” pentru a reprezenta rădăcina pătrată a cifrei -1. Aceasta se numește unitatea imaginară, nu este un număr real, nu există în viața „reală”, însă, poate fi folosită pentru a afla rădăcinile pătrate ale numerelor negative.
Până în epoca modernă, așa cum s-a întâmplat și pentru alte descoperiri din domeniul matematicii, numerele complexe au avut interes pur academic. Acestea se dovedesc a fi foarte utile în analiza informațiilor transmise prin unde, precum radiațiile electromagnetice, pe care le folosim în radio și wifi, semnale audio pentru muzică, telecomunicații și surse de curent alternativ.
În egală măsură, fizica cuantică reduce toate particulele la forme de undă, ceea ce înseamnă că numerele complexe sunt cruciale pentru a înțelege tehnologia din prezent, care ne-a permis, de fapt, să ne bucurăm de computerele moderne, fibra optică, GPS-ul, imaginile provenite de la RMN etc.